Exercise 3: Exploratory Data Analysis - Solution

Getting started

Load in the packages the you think you need for this exercise. You will be doing PCA, so have a look at which packages we used in Presentation 3. No worries if you forget any, you always load then later on.

library(tidyverse)
library(readxl)
library(FactoMineR)
library(factoextra)

Read in the joined diabetes data set you created in Exercise 2. If you did not make it all the way through Exercise 2 you can find the dataset you need in ../data/exercise2_diabetes_glucose.xlsx.
Have a look at the data type (numeric, categorical, factor) of each column to ensure these make sense. If need, convert variables to the correct (most logical) type.

diabetes_glucose <- read_xlsx('../data/exercise2_diabetes_glucose.xlsx')

diabetes_glucose

# A tibble: 1,422 × 13
   ID    Sex      Age BloodPressure   BMI PhysicalActivity Smoker  Diabetes
   <chr> <chr>  <dbl>         <dbl> <dbl>            <dbl> <chr>      <dbl>
 1 34120 Female    28            75  25.4               92 Never          0
 2 34120 Female    28            75  25.4               92 Never          0
 3 34120 Female    28            75  25.4               92 Never          0
 4 27458 Female    55            72  24.6               86 Never          0
 5 27458 Female    55            72  24.6               86 Never          0
 6 27458 Female    55            72  24.6               86 Never          0
 7 70630 Male      22            80  24.9              139 Unknown        0
 8 70630 Male      22            80  24.9              139 Unknown        0
 9 70630 Male      22            80  24.9              139 Unknown        0
10 13861 Female    56            72  37.1               64 Unknown        1
# ℹ 1,412 more rows
# ℹ 5 more variables: Serum_ca2 <dbl>, Married <chr>, Work <chr>,
#   Measurement <chr>, `Glucose (mmol/L)` <dbl>

Check Data Distributions

Let’s have a look at the distributions of the numerical variables.

Make histograms of the three Glucose (mmol/L) measurements in your dataset. What do you observe? Are the three groups of values normally distributed?

ggplot(diabetes_glucose, aes(x = `Glucose (mmol/L)`)) +
  geom_histogram(bins = 30, fill = "#482878FF", color = "white") +
  theme_minimal() +
  facet_wrap(vars(Measurement), nrow = 2, scales = "free")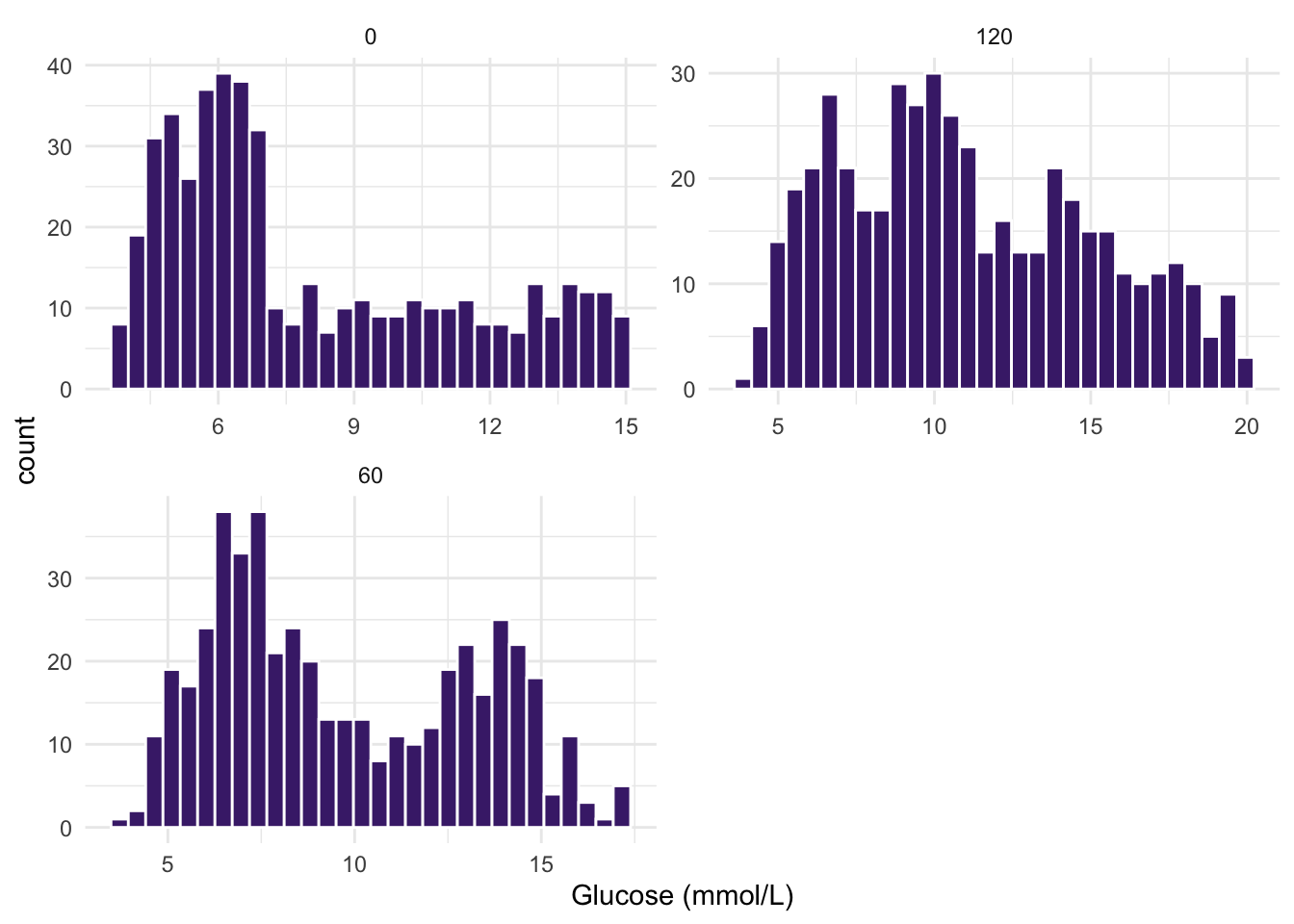

Just as in question 3 above, make histograms of the three Glucose (mmol/L) measurement variables, BUT this time stratify your dataset by the variable Diabetes. How do your distributions look now?

Hint

Try: facet_wrap(Var1 ~ Var2, scales = "free").

ggplot(diabetes_glucose, aes(x = `Glucose (mmol/L)`)) +
  geom_histogram(bins = 30, fill = "#482878FF", color = "white") +
  theme_minimal() +
  facet_wrap(Diabetes ~ Measurement, nrow = 2, scales = "free")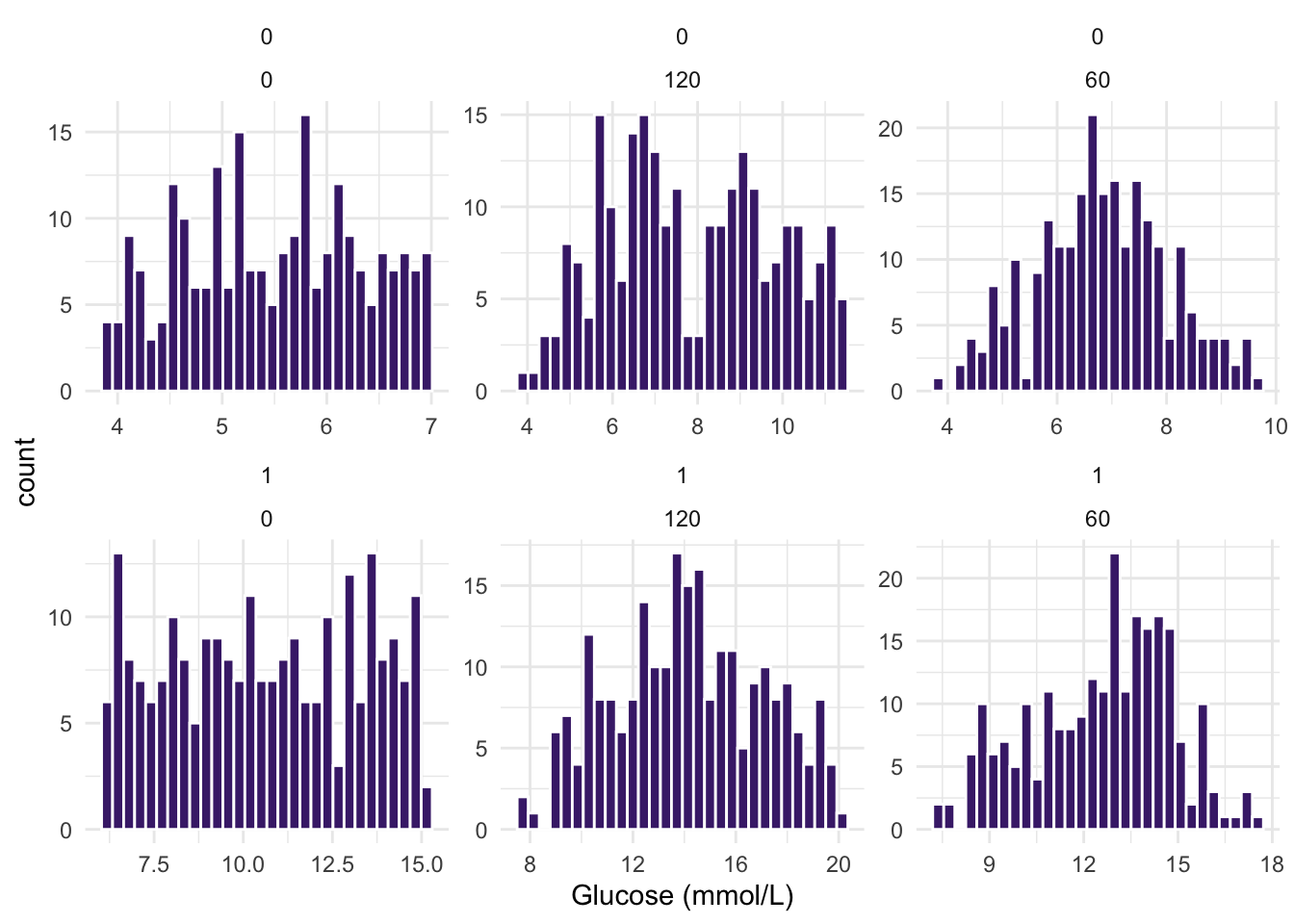

Make a qqnorm plot for the other numeric variables; Age, Bloodpressure, BMI, PhysicalActivity and Serum_ca2. What do the plots tell you?

df_long <- diabetes_glucose %>% 
  dplyr::select(Age, BloodPressure, BMI, PhysicalActivity, Serum_ca2)  %>%
  pivot_longer(cols = everything(),
               names_to = "variable", 
               values_to = "value")

# QQ plot
ggplot(df_long, aes(sample = value)) + 
  geom_qq_line(color = "magenta4") +
  geom_qq(alpha = 0.7, size = 0.5) +
  labs(title = "QQ Plot for Gene Expression",
       x = "Theoretical Quantiles", y = "Sample Quantiles") +
  theme_minimal() +
  facet_wrap(vars(variable), nrow = 2, scales = "free")

Warning: Removed 6 rows containing non-finite outside the scale range
(`stat_qq_line()`).

Warning: Removed 6 rows containing non-finite outside the scale range
(`stat_qq()`).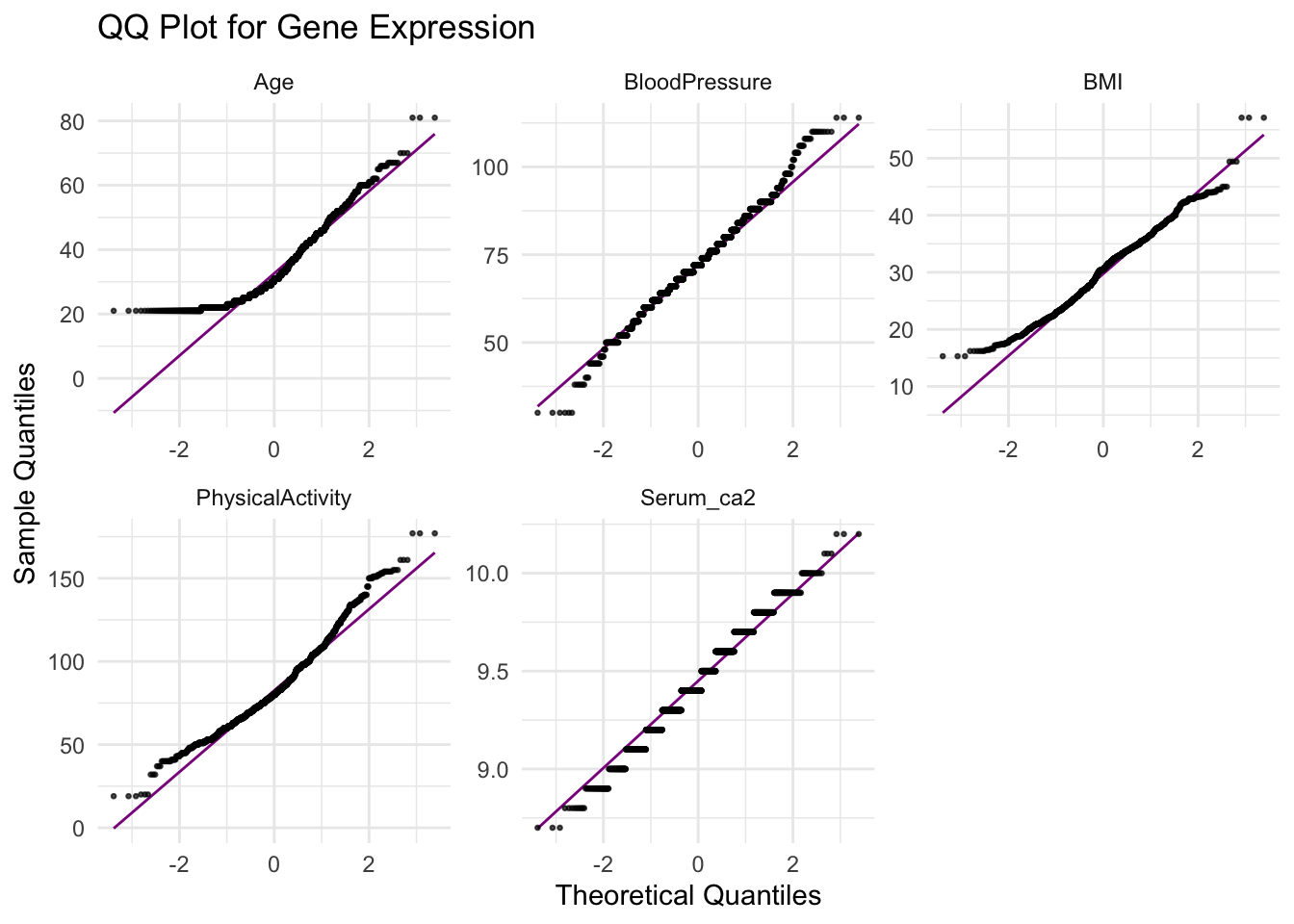

From the qq-norm plot above you will see that especially one of the variables seems to be far from normally distributed. What type of transformation could you potentially apply to this variable to make it normal? Transform and make a histogram or qqnorm plot. Did the transformation help?

ggplot(diabetes_glucose, aes(x = Age)) +
  geom_histogram(bins = 30, fill = "#A8D898", color = "white") +
  theme_minimal()

Warning: Removed 6 rows containing non-finite outside the scale range
(`stat_bin()`).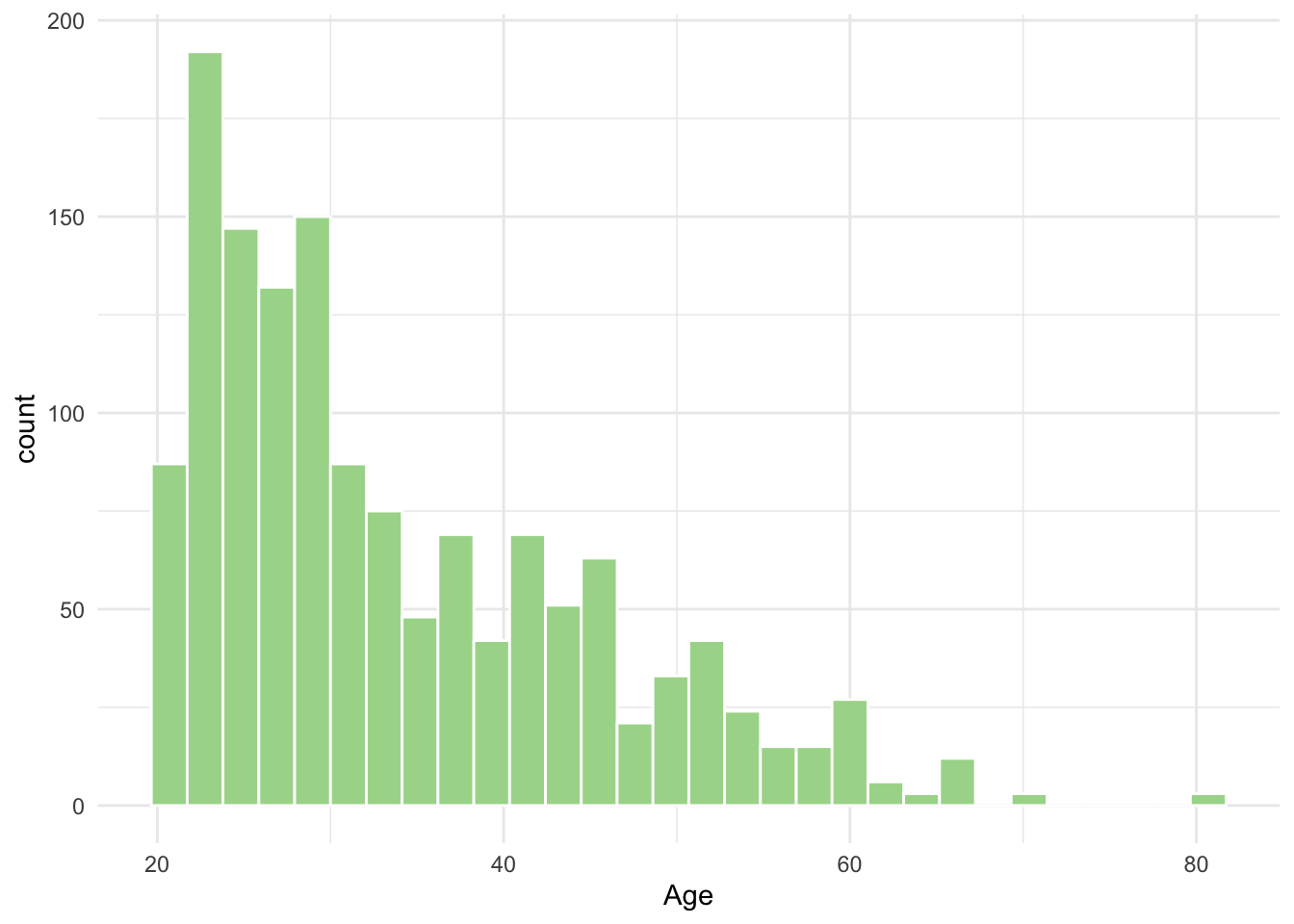

ggplot(diabetes_glucose, aes(x = log2(Age))) +
  geom_histogram(bins = 30, fill = "#A8D898", color = "white") +
  theme_minimal()

Warning: Removed 6 rows containing non-finite outside the scale range
(`stat_bin()`).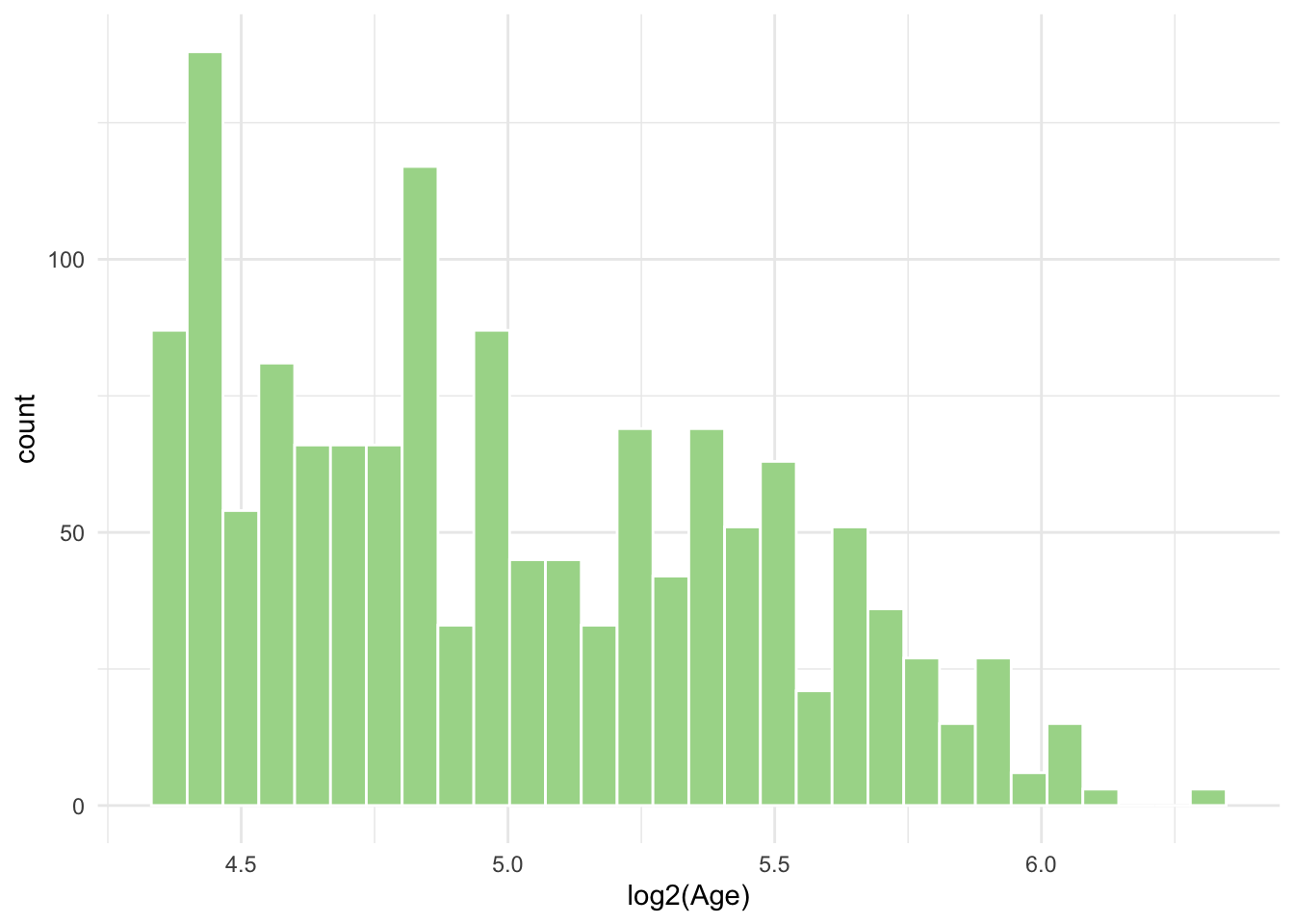

Luckily for us it is not a requirement for dimensionality reduction methods like PCA that neither variables nor their residuals were normally distributed. Requirements for normality becomes important when performing statistical tests and modelling, including t-tests, ANOVA and regression models (more on this in part 5).

Data Cleaning

While PCA is very forgiving in terms of variable distributions, there are some things it does not handle well, including missing values and varying ranges of numeric variables. So, before you go on you need to do a little data management.

The Glucose (mmol/L) variable in the dataset which denotes the result of the Oral Glucose Tolerance Test with measurements at times the 0, 60, 120 min should be separated out into three columns, one for each time point.

diabetes_glucose <- diabetes_glucose %>% 
  pivot_wider(names_from = Measurement,
              values_from = `Glucose (mmol/L)`,
              names_prefix = 'Measurement_')

diabetes_glucose

Remove any missing values from your dataset.

diabetes_glucose <- diabetes_glucose %>% 
  drop_na()

Extract all numeric variables AND scale these so they have comparable ranges. This numeric dataset you will use for PCA.

diab_glu_num <- diabetes_glucose %>% 
  dplyr::select(where(is.numeric)) %>%
  scale()

head(diab_glu_num)

            Age BloodPressure        BMI PhysicalActivity  Diabetes  Serum_ca2
[1,] -0.5095355    0.18808364 -0.7123872       0.31233047 -1.003892  0.6085078
[2,] -0.5095355    0.18808364 -0.7123872       0.31233047 -1.003892  0.6085078
[3,] -0.5095355    0.18808364 -0.7123872       0.31233047 -1.003892  0.6085078
[4,]  1.8586337   -0.04390803 -0.8322613       0.07595423 -1.003892 -0.9482168
[5,]  1.8586337   -0.04390803 -0.8322613       0.07595423 -1.003892 -0.9482168
[6,]  1.8586337   -0.04390803 -0.8322613       0.07595423 -1.003892 -0.9482168
     Glucose (mmol/L)
[1,]       -1.0027491
[2,]       -1.0027491
[3,]       -1.0027491
[4,]       -1.1514897
[5,]       -0.7756125
[6,]       -0.2183909

Extract all categorical variables from your dataset and save them to a new object. You will use these as labels for the PCA.

diab_glu_cat <- diabetes_glucose %>% 
  dplyr::select(where(is.character), Diabetes) %>% 
  mutate(Diabetes = as.factor(Diabetes))

head(diab_glu_cat)

# A tibble: 6 × 7
  ID    Sex    Smoker Married Work         Measurement Diabetes
  <chr> <chr>  <chr>  <chr>   <chr>        <chr>       <fct>   
1 34120 Female Never  No      Public       0           0       
2 34120 Female Never  No      Public       60          0       
3 34120 Female Never  No      Public       120         0       
4 27458 Female Never  No      SelfEmployed 0           0       
5 27458 Female Never  No      SelfEmployed 60          0       
6 27458 Female Never  No      SelfEmployed 120         0

Principal Component Analysis

Calculate the PCs on your numeric dataset using the function PCA() from the FactoMineR package. Note that you should set scale.unit = FALSE as you have already scaled your dataset.

res.pca <- PCA(diab_glu_num, graph = FALSE)

res.pca

**Results for the Principal Component Analysis (PCA)**
The analysis was performed on 1416 individuals, described by 7 variables
*The results are available in the following objects:

   name               description                          
1  "$eig"             "eigenvalues"                        
2  "$var"             "results for the variables"          
3  "$var$coord"       "coord. for the variables"           
4  "$var$cor"         "correlations variables - dimensions"
5  "$var$cos2"        "cos2 for the variables"             
6  "$var$contrib"     "contributions of the variables"     
7  "$ind"             "results for the individuals"        
8  "$ind$coord"       "coord. for the individuals"         
9  "$ind$cos2"        "cos2 for the individuals"           
10 "$ind$contrib"     "contributions of the individuals"   
11 "$call"            "summary statistics"                 
12 "$call$centre"     "mean of the variables"              
13 "$call$ecart.type" "standard error of the variables"    
14 "$call$row.w"      "weights for the individuals"        
15 "$call$col.w"      "weights for the variables"

Make a plot that shows how much variance is captured by each component (in each dimension). There are two ways of making this plot: either you can use the function fviz_screeplot() from the factoextra package as we did in the exercise OR, you can use ggplot2, by extracting the res.pca$eig and plotting the percentage of variance column.

PC_df <- as.data.frame(res.pca$eig) %>% 
  rownames_to_column(var = 'components')

labs <- round(PC_df$`percentage of variance`, digits = 2) %>% 
  as.character()

ggplot(PC_df, aes(x=components, y=`percentage of variance`, fill = eigenvalue)) + 
  geom_col() +
  theme_minimal() + 
  geom_text(aes(label = labs), vjust = -0.5)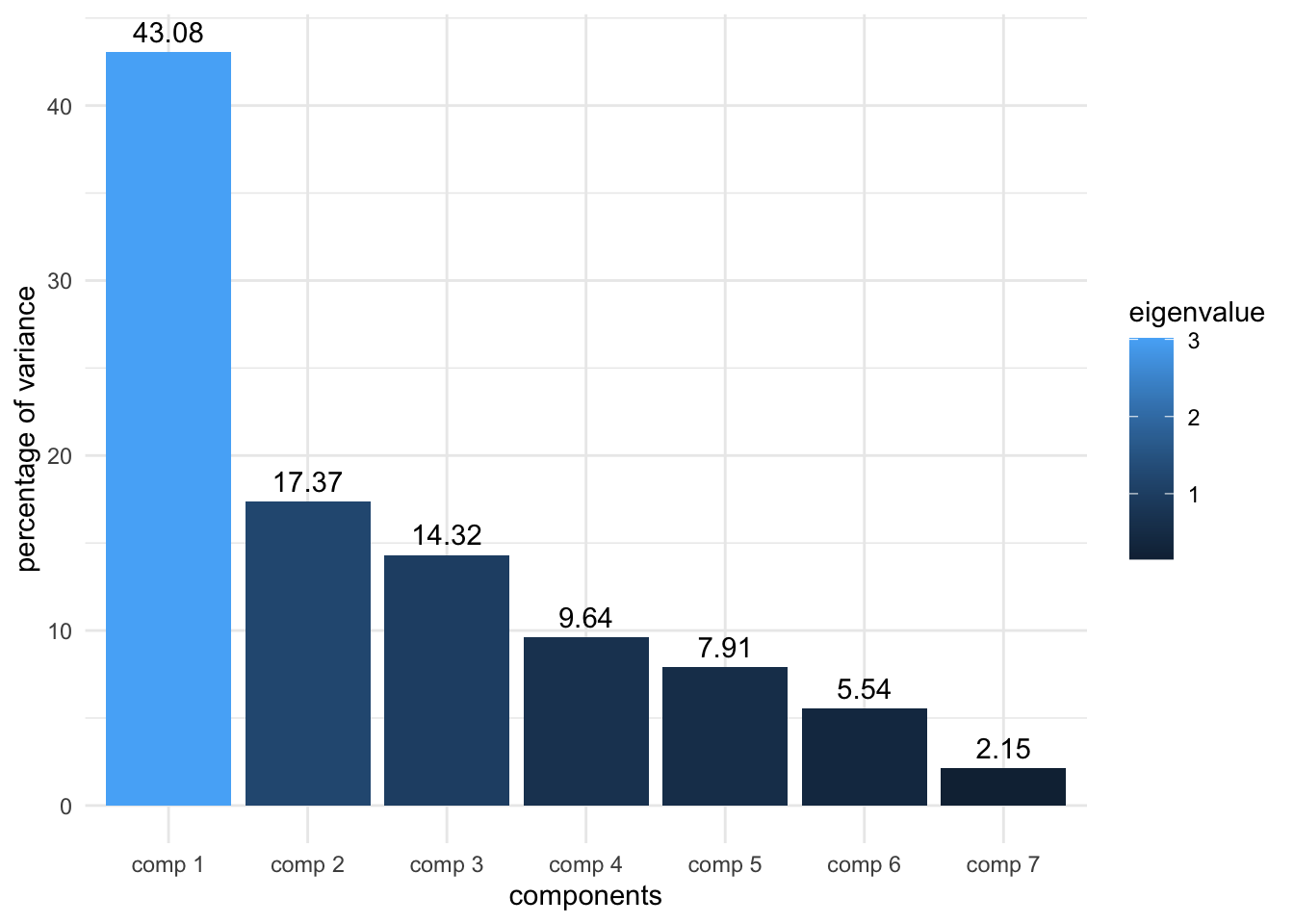

Now, make a biplot (the round one with the arrows we showed in the presentation). This type of plot is a little complicated with ggplot alone, so either use the fviz_pca_var() function from the factoextra package we showed in the presentation, or - if you want to challenge yourself - try autoplot() from the ggfortify package.

fviz_pca_var(res.pca, col.var = "cos2",
             gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"), 
             repel = TRUE) # Avoid text overlapping)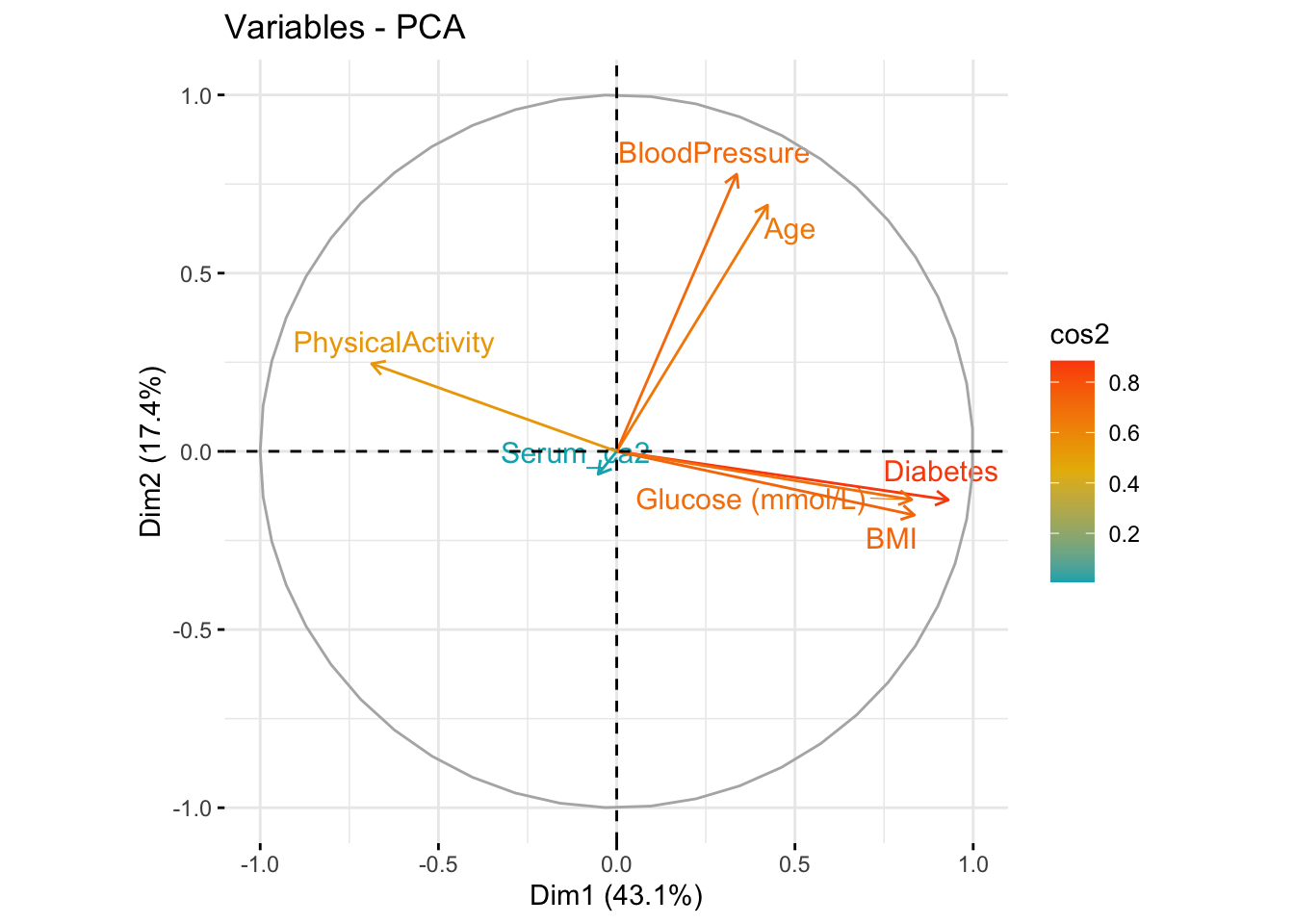

Have a look at the $var$contrib from your PCA object and compare it to the biplot, what do they tell you, i.e. which variables contribute the most to PC1 (dim1) and PC2 (dim2)? Also, look at the correlation matrix between variables in each component ($var$cor), what can you conclude from this?
Plot your samples in the new dimensions, i.e. PC1 (dim1) vs PC2 (dim2), with the function fviz_pca_ind(). Add color and/or labels to the points using categorical variables you extracted above. What pattern of clustering (in any) do you observe?

p1 <- fviz_pca_ind(res.pca, 
                   axes = c(1, 2), 
                   col.ind = diab_glu_cat$Diabetes,
                   geom = "point", 
                   legend.title = "Diabetes") + 
  scale_color_viridis_d() +
  theme(legend.position = "bottom")

p1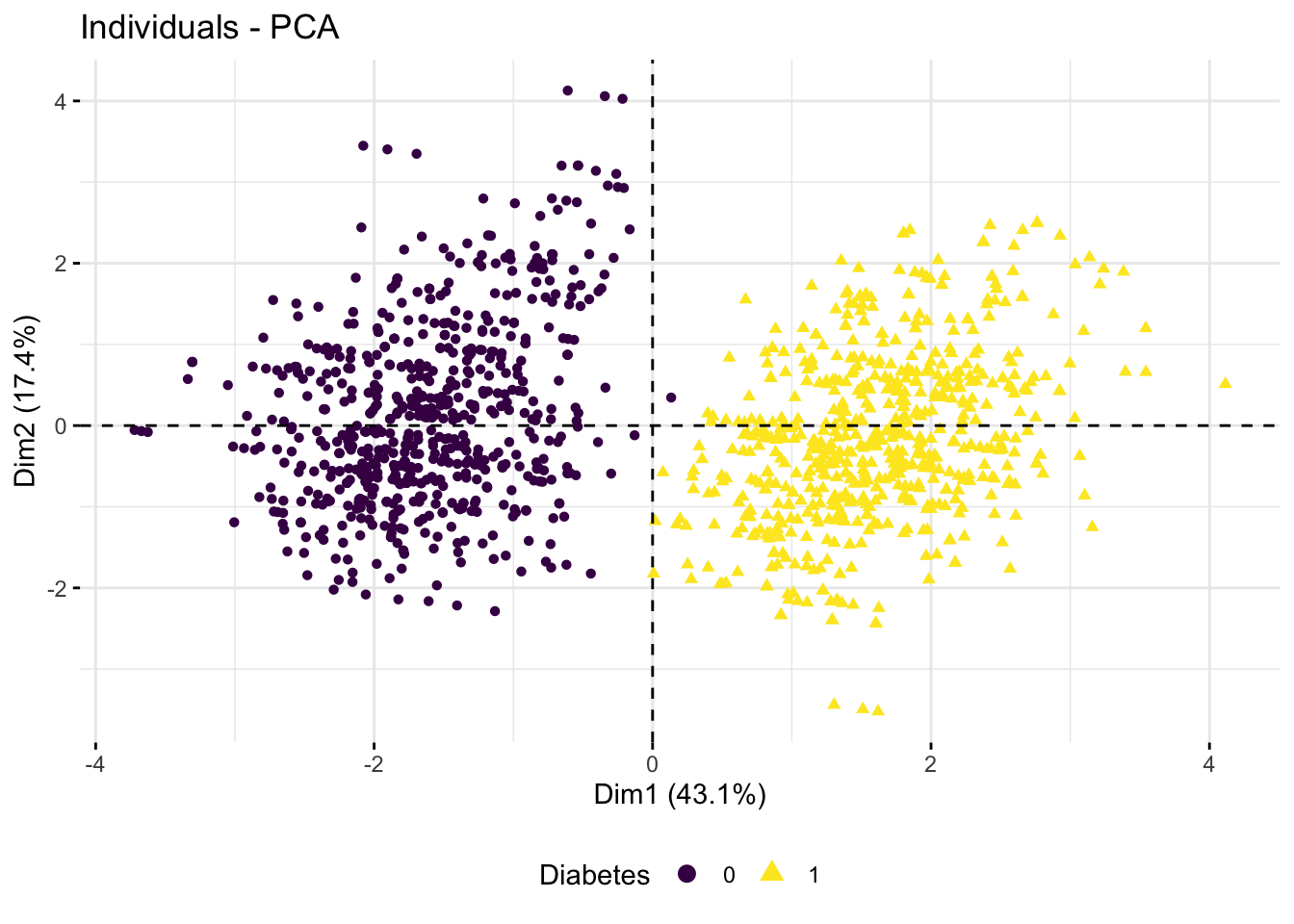

Try to call $var$cos2 from your PCA object. What does it tell you about the first 5 components? Are there any of these, in addition to Dim 1 and Dim 2, which seem to capture some variance? If so, try to plot these components and overlay the plot with the categorical variables from above to figure out which it might be capturing.

p1 <- fviz_pca_ind(res.pca, 
                   axes = c(1, 4), 
                   col.ind = diab_glu_cat$Smoker,
                   geom = "point", 
                   legend.title = "Smoker") + 
  scale_color_viridis_d() +
  theme(legend.position = "bottom")

p1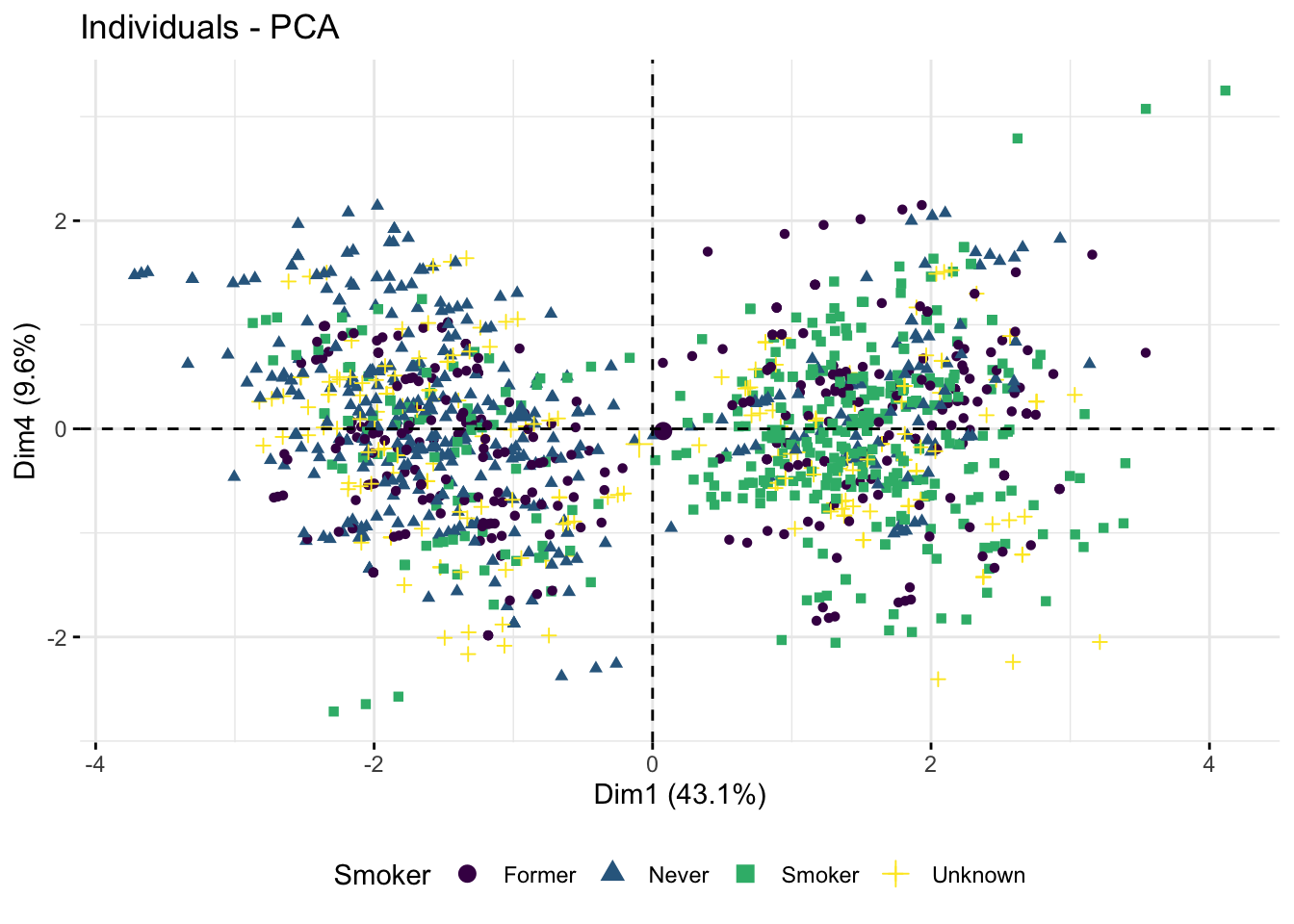

The Oral Glucose Tolerance Test is the one used to produce the OGTT measurements (0, 60, 120). As these measurement are directly used to diagnose diabetes we are not surprised that they separate the dataset well - we are being completely bias.

Omit the Glucose measurement columns, calculate a PCA and create the plot above. Do the remaining variables still capture the Diabetes pattern?

diab_glu_num <- diabetes_glucose %>% 
  dplyr::select(Age,BloodPressure, BMI, PhysicalActivity, Serum_ca2) %>%
  scale()

head(diab_glu_num)

res.pca <- PCA(diab_glu_num, graph = FALSE)

res.pca$var$cos2

                       Dim.1      Dim.2        Dim.3       Dim.4        Dim.5
Age              0.179044228 0.47738224 1.179010e-02 0.237077768 0.0822648503
BloodPressure    0.113238994 0.60479871 2.125569e-06 0.156507251 0.1174344511
BMI              0.697020728 0.03199509 6.799622e-04 0.066308130 0.0018402460
PhysicalActivity 0.472545917 0.06049427 5.974280e-03 0.186643304 0.2670768712
Diabetes         0.865617192 0.01854276 1.265714e-05 0.004176319 0.0085933098
Serum_ca2        0.002695452 0.00411849 9.832735e-01 0.009567730 0.0002967391
Glucose (mmol/L) 0.685119304 0.01840264 7.080813e-04 0.014552326 0.0759039042

fviz_pca_var(res.pca, col.var = "cos2",
             gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"), 
             repel = TRUE)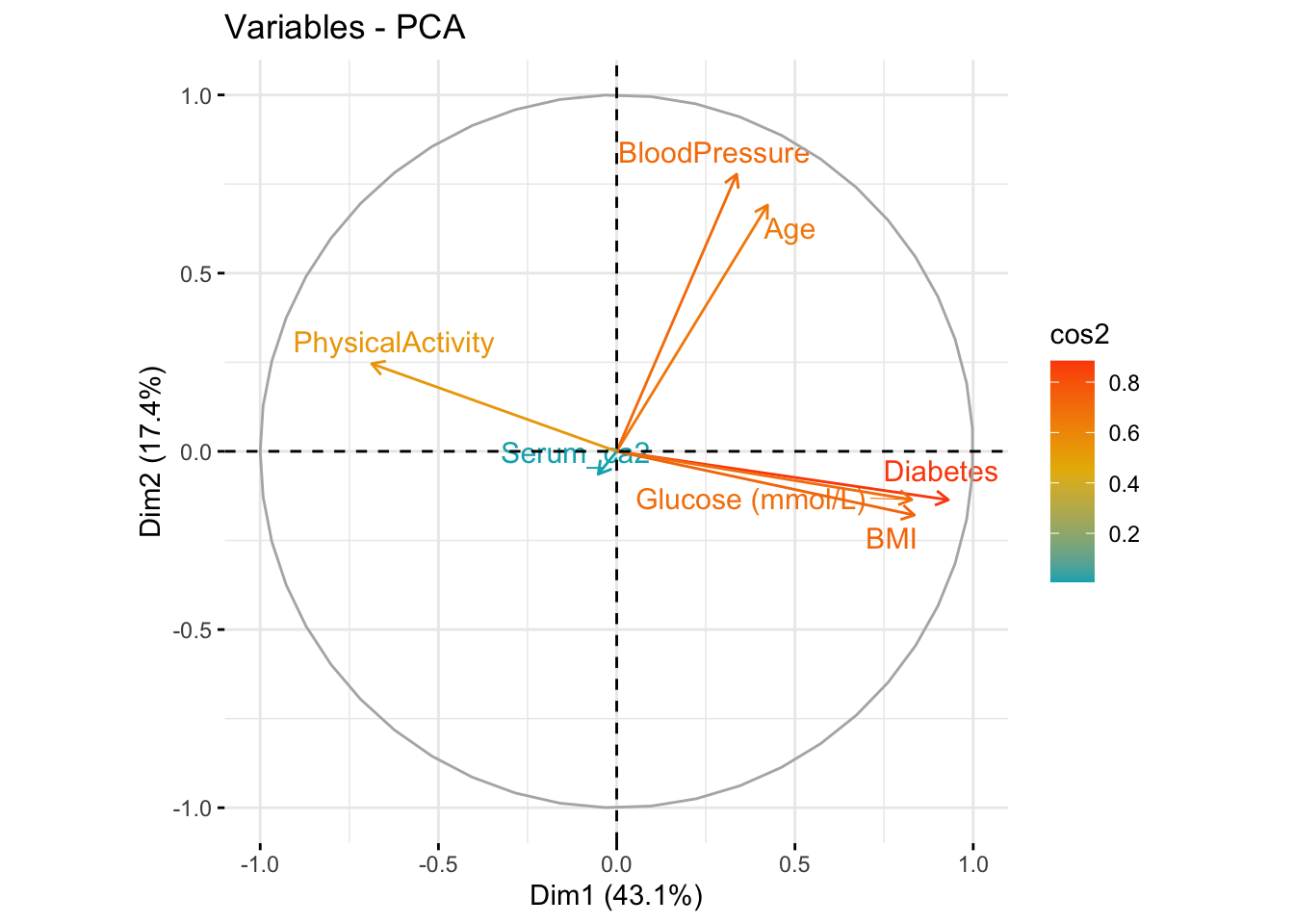

fviz_pca_ind(res.pca, 
             axes = c(1, 2), 
             col.ind = diab_glu_cat$Diabetes,
             geom = "point", 
             legend.title = "Diabetes") + 
  scale_color_viridis_d() +
  theme(legend.position = "bottom")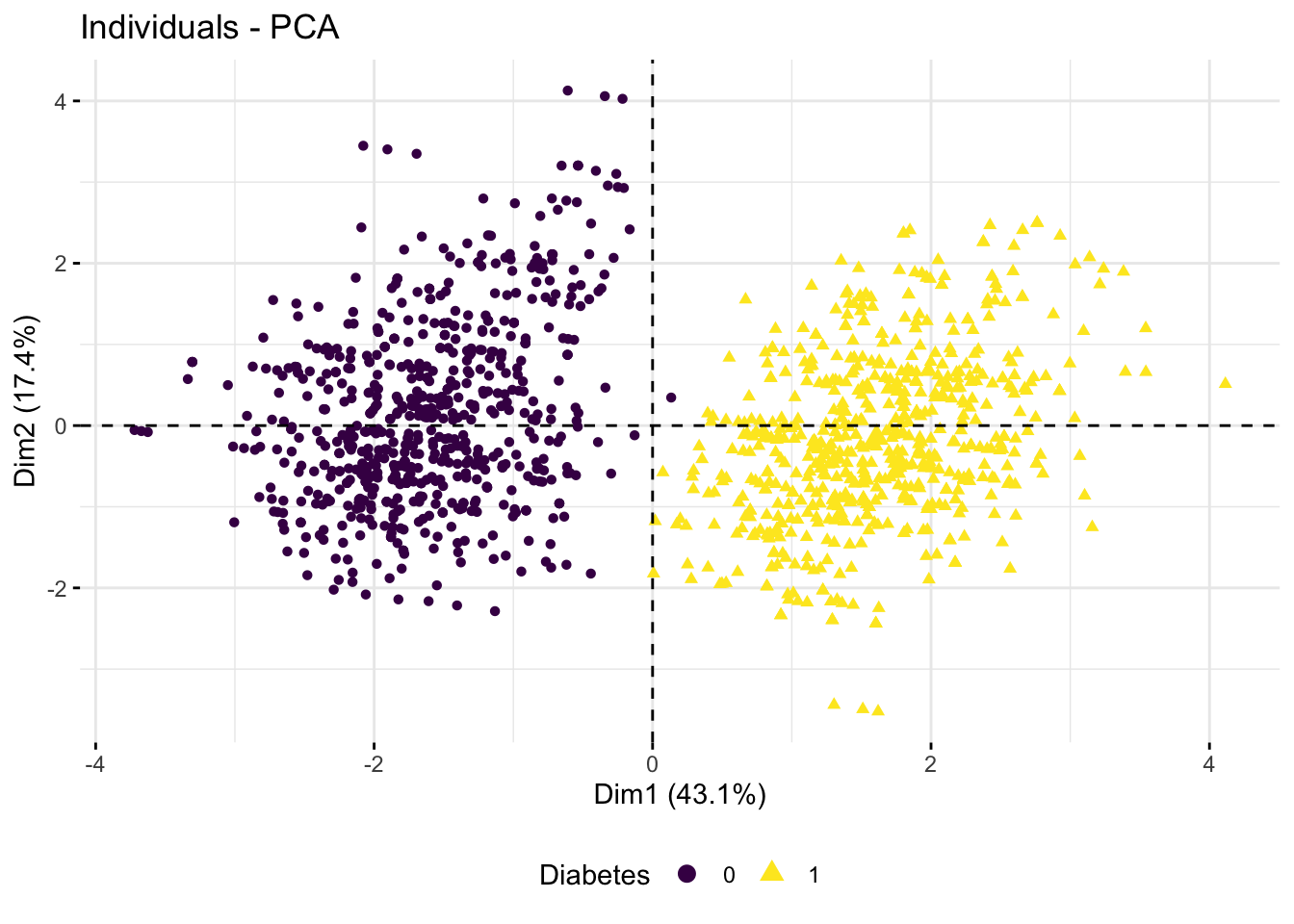

From the exploratory analysis you have performed, which variables (numeric and/or categorical) would you as a minimum include in a model for prediction of Diabetes? N.B again you should not include the actual glucose measurement variables as they where used to the define the outcome you are looking at.

diab_model <- lm(Diabetes ~ PhysicalActivity + BMI + BloodPressure + Smoker, data = diabetes_glucose)

summary(diab_model)


Call:
lm(formula = Diabetes ~ PhysicalActivity + BMI + BloodPressure + 
    Smoker, data = diabetes_glucose)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.98302 -0.17105  0.00882  0.21386  0.60857 

Coefficients:
                   Estimate Std. Error t value Pr(>|t|)    
(Intercept)      -0.6850976  0.0653602 -10.482  < 2e-16 ***
PhysicalActivity -0.0047429  0.0003280 -14.459  < 2e-16 ***
BMI               0.0456946  0.0012681  36.035  < 2e-16 ***
BloodPressure     0.0026039  0.0005694   4.573 5.23e-06 ***
SmokerNever      -0.0829057  0.0202943  -4.085 4.65e-05 ***
SmokerSmoker      0.1329873  0.0198258   6.708 2.85e-11 ***
SmokerUnknown     0.0147172  0.0238776   0.616    0.538    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.2712 on 1409 degrees of freedom
Multiple R-squared:  0.7073,    Adjusted R-squared:  0.7061 
F-statistic: 567.6 on 6 and 1409 DF,  p-value: < 2.2e-16